三角定規は、２種類あります。
　30°60°90°の直角三角形（半正三角形）と45°45°90°の直角二等辺三角形の２つです。
　なぜ、この角度にしたかといえば、高校の三角比に使えるからだそうです。
　30°は３分１直角、45°は２分の１直角、60°は３分の２直角となります。
　授業の流れとしては、最初に、30°の直角三角形で知ってることや気付いたことを発表させます。この中で、３つの角の大きさの和が180°になることも出るでしょう。ここは挙手発言でいきます。
　次に、45°の直角三角形で知ってること・気付いたことを箇条書きさせます。
　これは列指名で発表させ、それ以外の意見を挙手発言させます。
　ここで２つの気付きから出た共通意見として、「三角定規の３つの角の大きさの和は180°である。」を板書し、確認します。そして、三角定規の下に（三角形）と書き込み、「三角定規以外の三角形の３つの角の大きさの和も180°だろうか」と問いかけるのです。
　予想を言わせたあと、ノートに適当な三角形を描き、３つの角の大きさの和を求める式を書かせていきます。
　それらのノートを画面に映して紹介していきます。
　ただ、適当な三角形は、角度を測るのが難しいです。
　そこで、自分で２つの角を決めながら描いて、残りの角との和が180°になるかを確かめてもいいのです。
　例えば、10°70°と描けば、残りの角は100°になるわけです。
　問題になるのが、最後の問いです。
「分度器を使わないで、三角形の３つの角の大きさの和が180°になることを
　証明できますか。」
　証明という言葉は難しいので、「いえますか」にするかもしれません。
　教科書（学校図書）では、次の３つの方法が紹介されています。

1)３つの角を切り取って、それぞれの頂点を１つに集める。
2)合同な三角形をしきつめる。
3)三角形を折って３つの角をくっつける。

　私は、右のような方法を思いつきました。（思い出したのかも。）
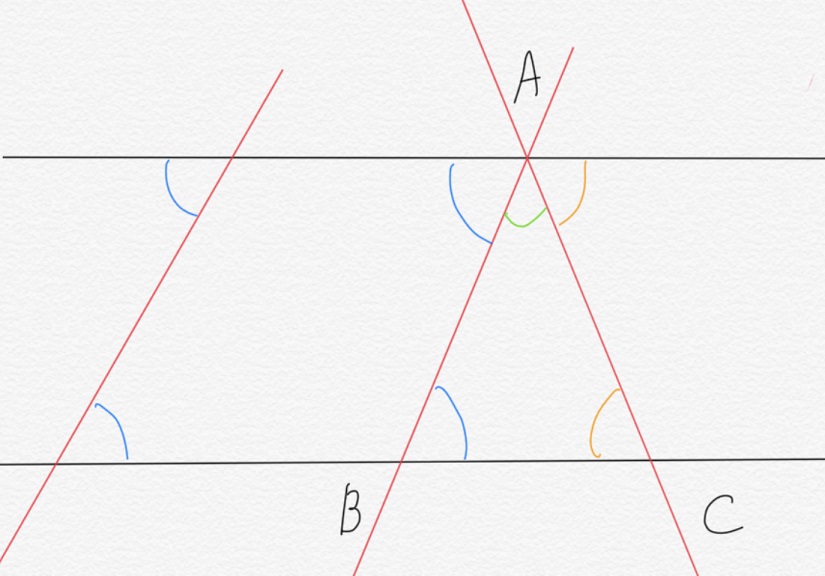
　平行な２本の直線にまたがるように引いた直線では、錯角が同じ角度になります。
　それを利用すれば、三角形の３つ角の大きさが180°であることは証明できるのです。
　子どもから出たら、すごいですが。

（2016.6.5）