昨日から「比例」の学習に入っています。

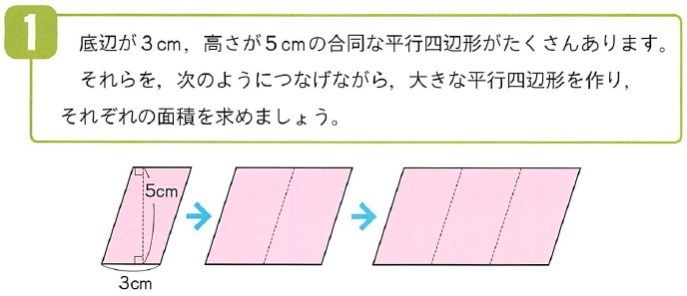
　上記の問題であれば、まず平行四辺形の面積を求める公式を書かせます。
　平行四辺形の面積＝底辺×高さ
「変わらないところはどこですか。」「高さです。」
　高さに赤下線を引き、５cmを１行下に書き、面積を○㎠、底辺を□cmの式で、式を書かせます。
　○㎠＝□cm×5cm
　このあと、教科書の表を埋めさせ、発表。
「平行四辺形の底辺と面積は比例していますか、していませんか。」
と、挙手確認をします。
　全員が比例に手を挙げます。
「なぜ、比例しているか理由を言える人？」
「平行四辺形の底辺が２倍、３倍すると、面積も２倍、３倍する。」
と言えればＯＫです。
「面積÷底辺をすると、いつも決まった数になるから。」
という子もいます。でもそれは、６年レベルの答えなのです。
　今回の比例は、グラフを書きません。詳しくは６年生でやるのです。
　次のページは、直方体の問題です。やり方は、同じです。

1)直方体の体積を求める公式を書く。　　　　　直方体の体積＝たて×横×高さ
2)変わらないところは何かを確認する。
3)変わらないところの長さを確認する。　　　　　　○㎤　　＝5cm×6cm×□cm
4)○と□を使って式を作る。
5)表を埋める。
6)直方体の高さと体積が比例しているか確認し、その理由を言わせる。

　直方体の体積が300㎤のとき、高さが何かを求めさせます。
　すると、多くの子は計算で求めてきます。
　でも、比例の考えを使うと簡単に求められるのです。（下のように）

　高さ　1cm →10倍→　□cm
　体積　30㎤ →10倍→　300㎤

（2017.1.31）