右の表は、24km行くときの時速と時間の関係です。
　これも面積図を使うと分かりやすいです。なぜなら、速さの学習では、縦を速さ、横を時間、面積を道のりとしてきたからです。

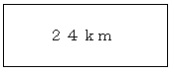
　それゆえ、左のような長方形を描き、その中に、きまっている道のり24kmを書き込みます。
　この後、「時速1kmだと何時間かかりますか」を問えば、24÷1で24時間という答えを導けます。
　逆も問えます。「３時間だと、時速何kmになりますか。」というように。
　そして、上の表で分かるように、時速は時間に反比例しています。
　要するに、面積図にしたときに、面積の部分がきまっている場合、それは反比例になるわけです。
　逆に、面積図にしたとき、縦の部分や横の部分が数のどちらが決まっていれば、それは比例になるわけです。
　比例と反比例の違いは、面積図でも分かるわけです。
（2015.10.20）