倍数と同じように、約数の見つけ方にもいろいろな方法があります。
　一番オーソドックスなのは、その数をその数までの整数で全て割ってみる方法です。
　割り切れるか割り切れないかを試していきます。例えば、12なら、

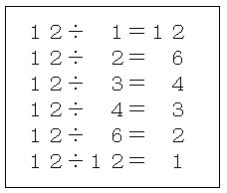
　１２÷　１＝１２　　　○
　１２÷　２＝　６　　　○
　１２÷　３＝　４　　　○
　１２÷　４＝　３　　　○
　１２÷　５＝　２…２　×
　１２÷　６＝　２　　　○
　１２÷　７＝　１…５　×
　１２÷　８＝　１…４　×
　１２÷　９＝　１…３　×
　１２÷１０＝　１…２　×
　１２÷１１＝　１…１　×
　１２÷１２＝　１ 　○
　１２の約数…１，２，３，４，６，１２

となります。右は、割り切れる式だけを載せたものです。
　割り切れる式だけ載せた場合は、わる数を上から順に並べて書けば、そのまま、その数の約数（小さい順）となります。
　多分、これが一番やりやすいでしょう。
　明治図書オンラインで検索したところ、松島博昭「［５年］約数を見つける基本型３種　「レインボー」「たてレインボー」「頂上チェック」」（『算数教科書教え方教室 2013年12月号』）に、頂上チェックというやり方が載っていました。
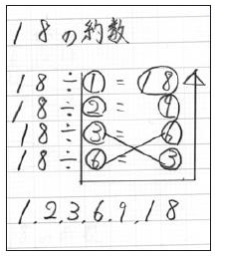
　わる数と答えがそれぞれ約数になることを確認してから、割り切れるわり算を書いていき、わる数と同じになる答えが出て来たら、そこまでで終わるという方法です。
　18の約数であれば、18÷6＝3をしたところで、同じ数が出て来たので、ここで終了となるのです。

　このやり方で、36の約数をすると、次のようになります。

36÷1＝36
36÷2＝18
36÷3＝12
36÷4＝ 9
36÷6＝ 6

　36÷6で答えに同じ6が出てきたので、終了。
　36の約数は、1,2,3,4,6,9,12,18,36の9個となるわけです。
　今日は、この頂上チェックを教えました。
　ただ、学習のしんどい子にとっては、このやり方よりも割り
　切れる式を全て書かせる方がいいのかもしれません。

（2016.9.5）