今日で、分数のひき算も終わりです。

　この問題が、分数のひき算で、一番難しい問題となります。
　式を立てるのは、簡単です。
　通分もすぐにできます。
　ただ、分子同士がこのままでは引けません。

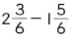
「どうしたらいいですか。」と聞くと、
「１くり下げたらいい。」という答えが返ってきます。

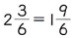
　左のように、直せばいいのです。
　でも、帯分数のくり下がりは、４年生で学習済みです。
　要するに、通分さえできれば、今まで習ったやり方でできるわけです。
　しかし、通分し、帯分数をくり下げ、さらに約分までするようになると、その途中のどこかで間違えてしまう場合があります。
　たんなるひき算を間違える場合もあれば、分母を３倍しているのに、分子を３倍するのを忘れてるということもあります。
　一つ一つの手順を丁寧にできることが、正しい結果につながるのです。

（2016.10.4）