明日から「体積」の学習に入ります。
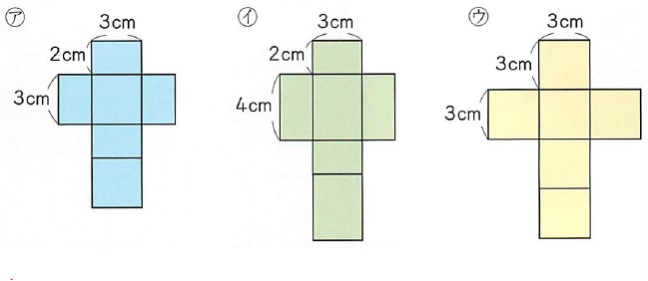
「３つのてん開図から、組み立てた箱があります。どの箱のかさがいちばん大き　いでしょうか。」
　この問題が学校図書での導入です。
　巻末には、右の展開図の画用紙版があり、組み立てられるようになっています。
　アとイ、アとウは、作った立体を直接比較することで、アの方が小さいことが分かります。問題は、イとウです。
（この展開の仕方は、いろいろなものの比べ方でよく出るパターンです。）
　塾で体積について学習している子は、縦×横×高さが体積になることを知っていて、イが3×2×4で24㎤、ウが3×3×3で27㎤なので、ウの方が大きいということを想定できるでしょう。
　それを揺さぶるような意見を教師としては持ちたい。
　教科書では、キャラクターが「たて、横、高さの３つの辺の長さの合計で比べると…。」と言っています。
　辺の長さの合計で比べると、箱のかさを比べることにつながるには、無理があります。
　では、てん開図の面積（表面積）はどうでしょうか。
　表面積で比べると、イは52㎠で、ウは56㎠です。
　表面積で比べてみても、ウの方が大きかったです。
　どうも揺さぶるような意見は見つかりません。
　では、かさを比べる方法をいくつも出させる方向でいけないでしょうか。
　例えば、それぞれの箱との同じ形を粘土でつくり、それを同じ形（例えば球）にすれば、大きさの違いを比べることができそうです。
　箱のフタを開け、そこに水を入れ、水の量を測るという方法もできます。
　水ではなく、砂を入れて、砂の量や重さで比べることもできそうです。
　それぞれの箱の重さを量ってみるのもいいでしょう。
　ただ、重さを量ることがかさの大きさを測ることにつながるかどうかが難しいです。なぜなら、子どもの作る箱は、中が空洞だからです。
　さらに、重さを量って比べられるのは、同じ材質のものである必要があります。
　鉄と木では、同じかさでも、鉄の方が重いことは子どもにも想像つくでしょう。
　金の王冠が、本当で金で造られているかを調べるために、アルキメデスは、王冠と同じ重さの金を水に沈め、あふれる水の量から調べたといいます。
　この逸話も話せたら話したいものです。

（2016.10.30）