分数÷整数の計算の求め方を考えさせました。

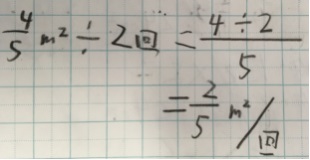
　一番、単純なのは、分子をそのままその整数でわるというものです。
　教科書の次の問題では、分子をその整数でわると、小数になります。

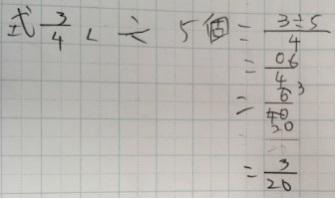
　それでもできないことはありません。
　小数になっても、整数になるように、分子と分母を10倍、100倍していけばいいのです。
　ただ、割り切れない場合は困るので、そのときは、この方法は使えなくなります。
　分数を小数にして求める方法もありました。

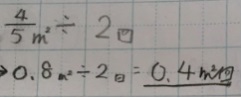
　ただ、これも割り切れない分数は、小数にできなくなってしまいます。
　分子÷整数の形にこだわるならば、分数をわる整数の数だけ分母も分子もかけて、それを元の整数でわる方法もあります。

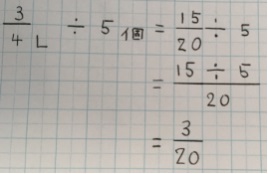
　これが実は、公式に一番近いといえます。
　分母と分子にわる整数の５をかけることで、分子のかけた５は５でわられて１となり、分子は元の数のままとなります。
　それゆえ、分母だけがわる整数でかけたことになるのです。

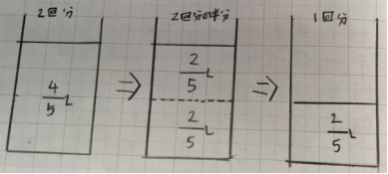
　最初の分数÷整数は、わる数が２なので、左のような単純な絵をかき、答えは簡単に求められます。
　ただ、５でわるときは、この絵が難しくなります。

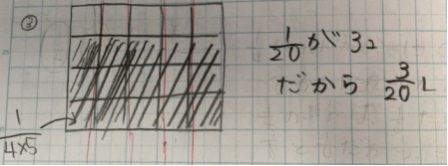
　４クラス中、１クラスだけ、わる５をたてにわって、答えを導き出していました。
　横にわっていたものをたてにわるという発想は、なかなか浮かばないようです。
　教科書のやり方も紹介して、最後は公式を紹介して、練習問題を解かすという流れになりました。なかなか腑に落ちるところまではいきませんでした。

（2016.11.28）